Tyto triky s čísly změní váš pohled na svět

Pět následujících problémů řešených alternativními postupy dokazuje, že u každé otázky nemusí být správné první řešení, které se nabízí. Vybrané příklady vás přesvědčí o tom, jak může být interpretace dat zavádějící a jak může vést k chybným závěrům.

1. Monty Hallova hádanka

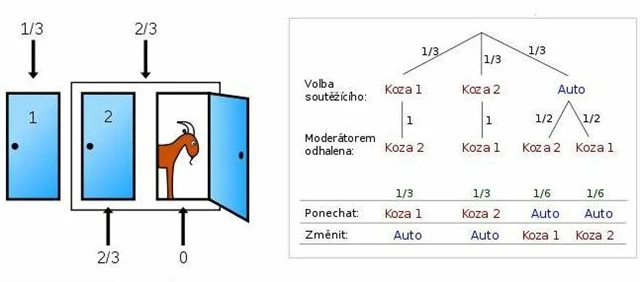
Tuto úlohu zadal svým soutěžícím moderátor Monty Hall v americké soutěži Let's Make a Deal. Spočívá v tom, že si má soutěžící vybrat z trojích dveří. Za jedněmi se skrývá hlavní cena (nové auto), další dvoje ukrývají cenu útěchy (kozu). Monty Hall poté, co soutěžící zvolí dveře, otevře vždy jedny s kozou. Následně má soutěžící možnost svou první volbu ještě dodatečně změnit na jiné dveře. Zvýší se tím pravděpodobnost výhry auta?

Ačkoli se na první pohled může zdát, že pravděpodobnost, že bude cena v původně zvolených dveřích, je padesát na padesát, statisticky se na to lze dívat z jiného úhlu:

V případě, že soutěžící zvolí jako první možnost dveře s kozou (což je pravděpodobné ze 66,67 %), změna mu vždy prospěje. Změna nebude výhodná pouze v případě, že měl štěstí a v původní volbě natrefil na auto (šance zvolit dveře s autem byla ale jen 33,33 %).

To znamená, že se ve dvou třetinách případů vyplatí dveře změnit.

2. Narozeninový paradox

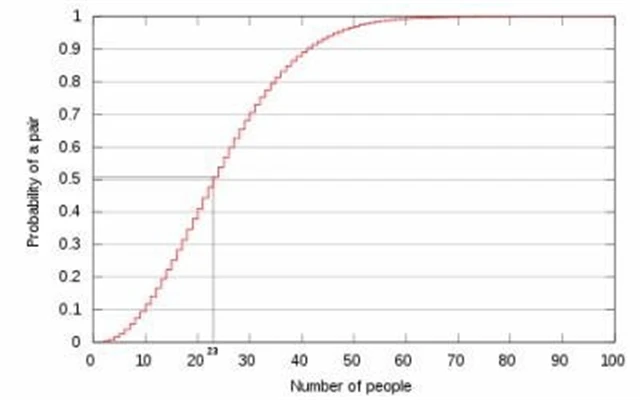
V kanceláři je 23 zaměstnanců. Jaká je pravděpodobnost, že budou mít dva zaměstnanci narozeniny ve stejný den? (Pro zjednodušení neuvažujme přestupný rok.)

Odpověď je zhruba 50 %.

Jakmile by bylo v kanceláři 366 lidí, bylo by jisté, že mají dva narozeniny ve stejný den, protože rok má pouze 365 dní. Protože neuvažujeme 29. února, pravděpodobnosti narozenin jsou pro všechny dny v roce rovnocenné. Kdyby bylo v kanceláři 57 lidí, byla by šance na společnou oslavu narozenin dvou kolegů 99 %.

Než abychom počítali pravděpodobnost, že dva lidé mají narozeniny ve stejný den, kalkulujme opak. Výsledek dostaneme, když získanou pravděpodobnost odečteme od jedné.

Šance dvou náhodně vybraných zaměstnanců, že nebudou mít narozeniny společně, je 364/365. Pravděpodobnost u třetí osoby bude 363/365. Pokud projdeme celou kancelář a vynásobíme zlomky, zjistíme, že pravděpodobnost, aby se narozeniny zaměstnanců ani v jednom případě nesešly ve stejný den, je 49,27 %:

365/365 x 364/365 x 363/365 x 362/365 x ... x 343/365 = 0,4927

Nyní číslo odečteme od jedné a přijdeme na to, že námi hledaná pravděpodobnost je 50,73 %.

3. Gamblerovo zoufalství

Hráč má určitou sumu peněz (B) a hraje hru, v níž je šance na výhru méně než jedna. Jakmile vyhraje, zvýší částku na zlomek B/N, přičemž N musí být kladné číslo (hodnotu sázky získá vydělením banku číslem N). Sázku neomezuje, pokud prohraje. Jakou výhru může očekávat, když se bude držet této strategie?

Ztratí všechno. Gambler je jen N prohraných sázek od bankrotu.

Myslíte, že by takhle sázel jen blázen? Uvědomte si, že jde o nejběžnější strategii v hazardních hrách. Kasína hráče při výhrách zásobují žetony s vysokými hodnotami, aby je povzbudili k vyšším sázkám.

Stejnou filozofii spatříte i v pokeru. Takzvaný blind - vstupní vklad na začátku téměř každé partie, se také nevrací, když prohrajete. Systém je navržen tak, aby urychlil vítězství úspěšných hráčů.

4. Poznatek Abrahama Walda

Abraham dostal za úkol prohlédnout zničená letadla, která se během druhé světové války po odletu z Německa vrátila, aby odhalil jejich slabá místa. Přišel na to, že nejnáchylnější na poškození od střel je trup a palivový systém. Co navrhl svým nadřízeným?

Ještě lépe chránit části, které nezaznamenaly poškození.

Abraham Wald, člen Statistické výzkumné skupiny, odhalil problém a přijal nekonvenční opatření, které následně zachránilo nespočet životů.

Jen samotný fakt, že se letadla vrátila, nasvědčuje tomu, že poničené části letadla tato poškození snesou. Pokud zůstává nejdůležitější část letadla soustavně bez poškození (jako například motor), je to pravděpodobně tím, že všechna letadla se zasaženým motorem nemohla dolétnout zpět.

5. Simpsonův paradox

Klinická studie se zabývá tím, jak dvě různé léčby (A a B) zabírají na malé a velké ledvinové kameny. Získala následné míry úspěšnosti:

• malé kameny, léčba A: 93 % (81 úspěšných z celkem 87 pokusů);

• malé kameny, léčba B: 87 % (234 úspěšných z celkem 270 pokusů);

• velké kameny, léčba A: 73 % (192 úspěšných z celkem 263 pokusů);

• velké kameny, léčba B: 69 % (55 úspěšných z celkem 80 pokusů);

• všechny kameny, léčba A: 78 % (273 úspěšných z celkem 350 pokusů);

• všechny kameny, léčba B: 83 % (289 úspěšných z celkem 350 pokusů).

Jaká léčba je lepší? A, nebo B?

Léčba A. Zjistíte to, když se zaměříte na dílčí soubory.

Ačkoli léčba A měla vyšší úspěšnost u malých i velkých kamenů, když se podíváte na celkový vzorek, zdá se být léčba B lepší. Je to tím, že léčba A byla výrazně častěji využívána u velkých kamenů, u nichž je postup složitější a méně často končí úspěchem.

Simpsonův paradox nám říká, že výsledky v dílčích skupinách vzorků nemusí nutně korelovat s výsledky celého souboru, což způsobuje nejednoznačnost. Skutečný příběh je potřeba hledat právě v podmnožinách.

Zdroj: Business Insider

Aktualita pro rok 2026